In 1997 the Department of Veterans Affairs (DVA) released the first version of a graphical user interface (GUI) for its flagship Electronic Medical Record (EMR) software called VistA (Veterans Health Information Systems and Technology Architecture). The graphical interface, called CPRS (Computerized Patient Record System) was based on client-server architecture, in which a graphical Windows client communicated with a VistA MUMPS database using remote procedure calls (RPCs).
The CPRS client program looked and functioned like a paper medical chart. CPRS was written in Delphi, then a Borland product, now Embarcadero. Before being introduced to CPRS I had no knowledge of client-server programming, or of remote procedure calls—or of Delphi. I recall a meeting session at which the original RPC broker developers described their product. At the time the RPC broker interested me more than its principle application did. To be able to harness the power of an immense database from an ordinary windows program seemed miraculous.

 The RPC broker (RPCB) was encapsulated as a Delphi component
that could be dropped onto a form in design view—of course the RPCB
was not a visual component. Its properties were similar to
those
shown on the right (this clip was
captured from the Embarcadero XE2 IDE as I
no longer have any Delphi IDEs).
The RPC broker (RPCB) was encapsulated as a Delphi component
that could be dropped onto a form in design view—of course the RPCB
was not a visual component. Its properties were similar to
those
shown on the right (this clip was
captured from the Embarcadero XE2 IDE as I
no longer have any Delphi IDEs).At first the DVA's VistA RPCB used a callback mechanism, perhaps to thwart unauthorized client access to the database. The client computer called the VistA MUMPS database server and then listened for a callback from the server (a separate connection). This method, which was awkward to implement between isolated private networks, was eventually abandoned, to be replaced by a direct-connect broker and augmented by other security measures.

While the RPC broker was primarily intended for use with Delphi,[0] the developers had also released a kit that could be used with Visual BASIC (VB). I had written some graphical Windows programs using Visual BASIC, and was keen to try out the RPCB in the VB programming environment. One of my early projects was a graphical front end for a point-of-care laboratory instrument interface to VistA, originally written for Windows 3.1 and Windows 95. The image on the left shows an anachronistic popup from that program. Later, I created a Delphi version.
Another VB program that I subsequently re-wrote in Delphi was an implementation of Pentominoes, a game that was originally described in Scientific American.[2] The Pentominoes project will be described in later paragraphs (it was not a broker application).
In the late 1990's Borland's Delphi was an attractive development environment for Windows. .NET had not yet been released. The Eclipse SDK was also in the future. At the time, VB seemed somewhat limiting and Delphi promised to be more flexible.
 There was also a Linux version of Borland Delphi called Kylix.
I
had a trial version of Kylix that would execute a program in the IDE
only.
At first I tried doing the same project concurrently in
Delphi
and Kylix, in order to get a feel for what worked the same and what was
different (winsock dependencies, etc). My first Delphi-Kylix
project did not involve the broker. It was intended to
control
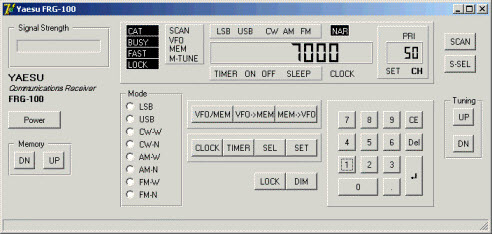
my shortwave radio receiver using a virtual front panel, a form that
resembled the actual front panel of the radio. Unfortunately I do not
have an image of the project as it appeared in the Kylix IDE, but it
was similar to the Delphi version (right).[1]
There was also a Linux version of Borland Delphi called Kylix.
I
had a trial version of Kylix that would execute a program in the IDE
only.
At first I tried doing the same project concurrently in
Delphi
and Kylix, in order to get a feel for what worked the same and what was
different (winsock dependencies, etc). My first Delphi-Kylix
project did not involve the broker. It was intended to
control
my shortwave radio receiver using a virtual front panel, a form that
resembled the actual front panel of the radio. Unfortunately I do not
have an image of the project as it appeared in the Kylix IDE, but it
was similar to the Delphi version (right).[1]Later I spent some time in an attempt to port the VistA RPC Broker to Kylix, but eventually gave up. My knowledge was not up to converting Windows socket API calls to equivalent Linux functionality.
The programming language of Delphi and its successors is Object Pascal. Pascal was once favored as an instructional language in colleges and universities. Recognizable or conspicuous features of Pascal code are the begin and end keywords that bound code blocks, like { and } in C or Java, as well as the symbol for the assignment operator := (colon followed by equals).
Different programming languages are more-or-less suited to different kinds of problems. Many programmers become attached to a particular language, favoring it to other languages for nearly anything that they do. I have never felt a strong allegiance to any programming language. Languages are tools with which to express ideas. Some are more suited than others for computation (mathematics), or for string-manipulation (text processing), or for database access, or for teaching students about objects, and so forth. Suitability to a particular type of problem does not make one language better or worse than another.
Many programming languages share a similar appearance and feature set. Of course, strange looking languages also exist—I recall the language APL (suited for manipulating matrices) that used a strange symbol set, but I digress. The point I want to make is that there is a great deal of positive transfer of knowledge between programming languages, more than for human languages—I think. Thus, a programmer familiar with one language can generally learn another with minimal effort. And the more programming languages one learns, the easier it is to learn a new one. Acquiring proficiency, though, does not equate to expertise in a language. Programming proficiency is more like learning to speak a human language. Learning to write a great book would be another matter.
When attempting to learn concepts and idiosyncrasies of a new programming language, my usual strategy has been to undertake a moderately complex project, begin to program it, and then look up anything that isn't obvious along the way. For the purpose of exploring a language, I typicially select a problem that I have not programmed before. However, as previously remarked I first programmed Pentominoes in Visual BASIC and then re-programmed it in Delphi, incorporating ideas and concepts from the original VB implementation.
Pentominoes - Among the many wonderful inventions that Martin Gardner introduced through his Mathematical Games column in Scientific American was a set of curious shapes called Pentominoes.[3] Pentominoes are the order 5 instance of a more general construct called “polyominoes,” shapes that are formed from a given number of congruent squares, each touching at least one other. Nearly everyone has seen one game that is based on polyominoes, namely Tetris![4]
Martin Gardner came to know about Pentominoes from Solomon W. Golomb,[5] then professor of electrical engineering at the University of Southern California. Professor Golomb published a book about these objects.[6] But long before I knew about or had read Golomb's book, I spent hours exploring the twelve shapes that can be made from five contiguous congruent squares, the objects called Pentominoes. Many web sites have illustrations of the Pentomino pieces, for example here.
In addition to the huge wealth of puzzles that suggest themselves almost naturally, and that are described in numerous articles and books, a two-player game can be played with pentominoes. The game’s rules were explained in one of Martin Gardner’s early columns. It is played on an ordinary chessboard with specially constructed pieces whose squares are congruent to board squares. “…players take turns placing a Pentomino piece on the board. The first player who is unable to play loses.”[7]
On first reading about the Pentominoes game, I tried playing it using a folding checkerboard and matching cardboard cutout pieces. The rule that “the first player who cannot place a piece loses” seemed unfair. If both players have succeeded in placing the same number of pieces when no more can be placed, then the player on turn (the first player) has lost. That did not seem right!
So for my own play, I changed the suggested rules to award each player a score for the game, equal to the number of pieces placed. The original game description did not specify a single method by which pieces were to be selected. “The players can play from a common pile of Pentominoes, or divide the 12 Pentominoes in some fashion at the beginning of the game, or even be required to play a random Pentomino drawn from a bag.”[8] That last suggestion seemed crazy. The players would need a third person to draw the shape; otherwise selection would not be random.
I thought that choosing pieces should be part of the game strategy, and that the players should take turns selecting from a pile before placing the first piece. If one particular piece was beneficial to have, then the player with the first choice would obtain an unfair advantage. This prompted the next specification in my adaptation of the rules. Games would be played in sets of four and scored as the total pieces placed by each player summed over the four-game set.

By the time the rules had evolved to encompass balanced sets, I had constructed a set of Plexiglas® pieces, and was playing games with chess buddies. Naturally we used a chess clock. The time control was 20 minutes per player per game, if recollection serves.
When I first began to play the game it did not occur to me that Pentominoes could be analyzed by computer—it probably could not at that time. Somewhat to my dismay, because it seems to diminish the game's interest a little, I recently learned that in 1996 Hilary Orman proved the original game to be a win for the first player.[9]
I will return to Orman’s proof later. Although the piece selection rules differ, it is likely that her proof also applies to the rules adaptation described in the preceding paragraphs, making the theoretical outcome for a set of games a tie. All interest is not lost, even if this is so. The analogous order-6 game “Hexominoes,” played on a 15 x 15 square board, remains unsolved, to the best of my knowledge.
According to old notes, I programmed Pentominoes in Visual BASIC in April 1995. “The VB project was called Pento.” My notes on the project include image clips that were printed on the black and white HP Laserjet IV printer.
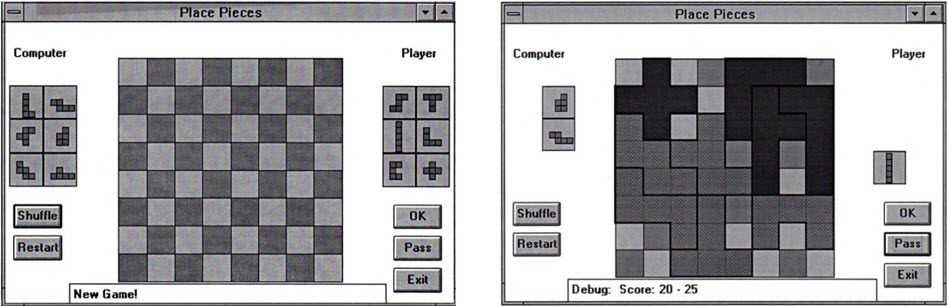
I was surprised when reviewing journal entries about Pento to find that the representation and display of pieces appeared to have been solved early in the design, although piece boundaries slightly overlap the board edge in the illustration. My notes suggest that the principal concern was to devise and code a practical playing strategy for the computer, so that it would stand a chance of winning, when playing against a human player.
My notes do not say (and I cannot remember) how the Pentomino pieces were constructed in the Visual BASIC implementation. However, I do recall how pieces were computed for the Delphi version, which also included Hexominoes, the order-6 game.
For the Delphi version (circa 2001), if not for the earlier VB program, pieces were computed in MUMPS, and then loaded into the Pentominoes program as pre-defined arrays. The method was probably inefficient, both in the way shapes were computed and in the way they were represented. Since then I have read in accounts of chess programming about the use of bit boards. The bit board object represents the 8 x 8 chessboard as a single 64-bit word (or two 32-bit words). Each square corresponds to one bit. Thus, for example, a single word of memory can theoretically specify the location of all pawns of one color in chess. This is efficient use of storage!
Here is how the MUMPS computation worked. First, to state the obvious, any Pentomino piece in any orientation, regardless of how it is rotated or flipped, fits within a 5 x 5 cell grid. Similarly, any hexomino piece, regardless of orientation fits in a 6 x 6 grid, and so forth. Let us carry this observation a little bit further.
A 5 x 5 grid consists of 25 squares. A Pentomino piece in a specified position and orientation consists of 5 squares contained within this grid. Now it is possible—I should say easy—to create a program that enumerates all of the 25C5 combinations of 25 grid cells taken 5 at a time. Furthermore, it is straightforward to identify which of these combinations represent connected cells and which do not. Thus by generating order-5 combinations, and discarding those that are not 5 connected cells, one can construct all the Pentominoes, their reflections, rotations, and translations, where translations correspond to positions in the grid.
To eliminate superfluous translations of the same piece, we define a canonic position, such as the lower left corner. For each combination that qualifies as a Pentomino piece, translate it as far down and to the left as it will go. And of course count identical results only once. This operation leads to the set of Pentominoes with reflections and rotations counted as distinct.
Finally, to eliminate reflections and rotations, it is only necessary to reflect and rotate each piece through the 2 x 4 = 8 possibilities, keeping the first instance, and discarding equivalent combinations. This process culminates with the familiar set of 12 Pentominoes.
Recently, I happened upon the original MUMPS procedure that computes N-ominoes in the way that is outlined above. The routine includes an option to display the computed objects as text-based graphics. For fun I ran the code to compute and graph the 35 hexominoes.

I will say more about Hexominoes later. At present for clarity’s sake I wish to point out that each piece may be identified by the relative coordinates of its grid squares (5 points for Pentominoes, 6 for Hexominoes, etc.). Thus, for example the piece shown in the lower left corner of the illustration above (bottom row, left column) can be represented {(1,1), (1,2), (2,2), (2,3), (3,3), (3,4)}.
As previously hinted, I have come to believe, based on reading about chess programming, that representing pieces in a board-centric way (or grid-centric, where the grid slides about the board) is probably inefficient. It may have been better to use piece-centric representations of the board. But that would have required a different way of thinking, which did not happen.
Returning briefly to the first (Visual BASIC) implementation of Pentominoes, my notes mention several subsidiary problems that had to be addressed. First, the program needed a way to organize empty cells (cells that remain after one or more pieces have been placed on the board). This would facilitate identification of areas that could be used to place remaining pieces, as well as dead areas.
To this end I defined a construct called “chain.” A chain could consist of either occupied or empty squares. For illustrative purposes I will explain only the “empty” case. Two empty squares (cells) were said to be connected if they differed by 1 in one coordinate and had the same value for their other coordinate. Generalizing connectedness to more than two squares, A and C were said to be connected if A was connected to B and B was connected to C. Using this recursive definition, squares (cells) could be classified into indexed maximally connected sets called chains. The number of cells in a chain was its order. (Empty-cell) chains of order less than 5 were dead, in the sense that no Pentomino piece could be placed there. Chains of order equal to 5 accommodated exactly one piece (but maybe one that had been placed previously). And so forth. Identification of chains and their orders was thus a crucial step in solving the computer’s playing strategy problem. My notes express frustration that this problem, which is solved instantaneously by human visualization, seems to require a time-consuming algorithm. Maybe that is when I should have thought of bit-boards!
In any case, indexing empty chains became a step in the evaluation process. For example, if after making a trial placement for a piece, the computer identified a new empty chain of index 5, it could then ascertain whether the chain belonged to one of its own remaining pieces (a sanctuary ++),[10] one of its opponent’s unplaced pieces (a potential gift to the opponent --) or a piece that was previously placed (requiring updating the order of the dead list, and then evaluating the parity of the number of pieces that could still theoretically be placed).
Sanctuaries are not necessarily exact. In other words a Pentominoes sanctuary could consist of more than 5 empty squares, and yet only accommodate one piece. For example, if the eight squares in one row (or column) are blocked off (completely bounded), then the straight piece (called the “I” pentomino) can be placed anywhere on the 8-cell row (or column) and no other piece can go there.
Notes on the Visual BASIC version of Pentominoes gradually became sparse. About a month after starting the project my notes record a look-ahead strategy to be used when play has progressed about half-way through the game. At this point it becomes computationally feasible to examine all possible continuations, leading to a forced best result for the computer from that point forward. I recall that the computer occasionally played surprising moves at this stage, but the notes contain no corroboration of this recollection.
One note describes a scheme for recording games, and another records implementation of a simulation mode, in which the program plays against itself. Simulation mode enabled the abandonment of heuristics that were intuitively plausible, but did not in fact improve the computer’s play. One such heuristic had the program attempt to disrupt a move in which its opponent could create a sanctuary on the next play. Surprisingly, this did not help!
I will briefly describe the Delphi implementation, which included a Hexominoes variant (not in the original VB version). The order-6 game is harder to visualize (more shapes and larger board). Plus, as far as I know it is not yet solved.
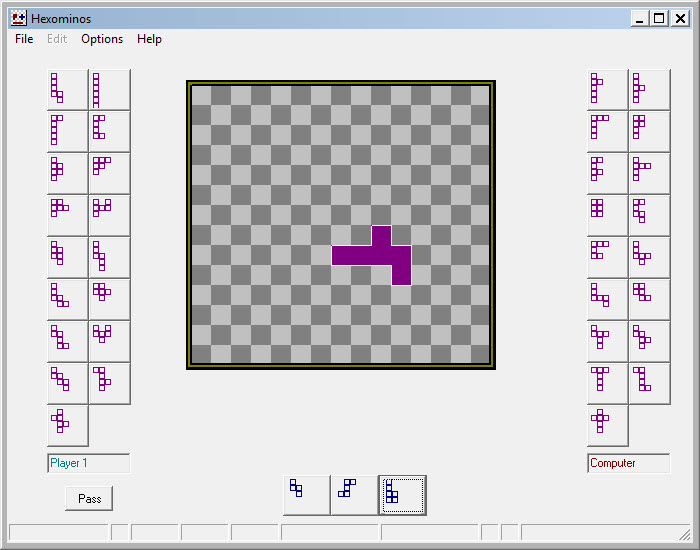
The screenshot above shows the start of a hexominoes game in the Delphi implementation, after the pieces have been shuffled and distributed to the two players. Because 35 is an odd number, the program has placed one piece randomly (but away from the edge of the board), so that the players will have the same number of pieces (17 each) for the game. The piece that has been placed before the beginning of play is colored differently from the game pieces, and does not count toward the score.

The screenshot above shows the same game after each player has placed 3 pieces. The status bar displays a current evaluation of the position as number of pieces placed “+” sanctuaries created by each player. Thus, in the example, the human player (green) has placed three pieces and created one sanctuary, while the computer (red) has placed three pieces and created two sanctuaries. It is the human player’s turn.
The image below shows the same game at a later point. At this stage, the computer has created two more sanctuaries than the human player. However, first appearances may be deceiving.

The final result was a tie (below), possibly because the human player paid attention to unprotected shapes remaining in the computer’s pile, and deliberately disrupted potentially useable empty chains. But then, maybe it was luck!

The Delphi implementation improved on the Visual BASIC user interface but made few changes to the original game logic, other than to support the order-4 and -6 games. The objective was more about learning Delphi than about revising the program's design.
It is not easy to decide upon a “best” board configuration for playing a given order of polyominoes. Many puzzles use non-square boards, but I prefer square. If both players succeed in placing all their Hexominoes pieces on the 15 x 15 board, a total of 15 empty squares remain. This may seem a large number—surely it favors successful placement… But not so! In practice, at least in my experience, it is rare for both players to place all of their pieces in Hexominoes—I cannot recall a single such instance.
Finally, a note about Hilary Orman’s Pentominoes proof… Orman had created a program in the C language to play Pentominoes, and had also acquired an understanding of the moves that maximally restrict subsequent play. This way of thinking differs from the strategy of creating sanctuaries for one’s own pieces. It is more analogous to the strategy of tracking the total order of dead chains. Perhaps the reason for this approach is that, in the original game, players selected pieces from a common pile and placed them immediately. The players did not “own” pieces for which to create sanctuaries.
So how could Orman’s proof relate to the situation in which players choose pieces in advance? First, Orman proved that more than one first move involving more than one piece was a win for the first player. After she had proved the win based on a good-guess first move, she tried additional “good-guess” first moves.
Thus, the player who will have the first turn at placing a piece can choose a winning piece on his first selection, whether or not his opponent has already selected a “winning” piece.
Concretely, both of the first moves shown below (reproduced from Orman’s paper) are winning. Thus whether the player who places first has the right of first choice or second choice, he/she can select a piece and place it to win.
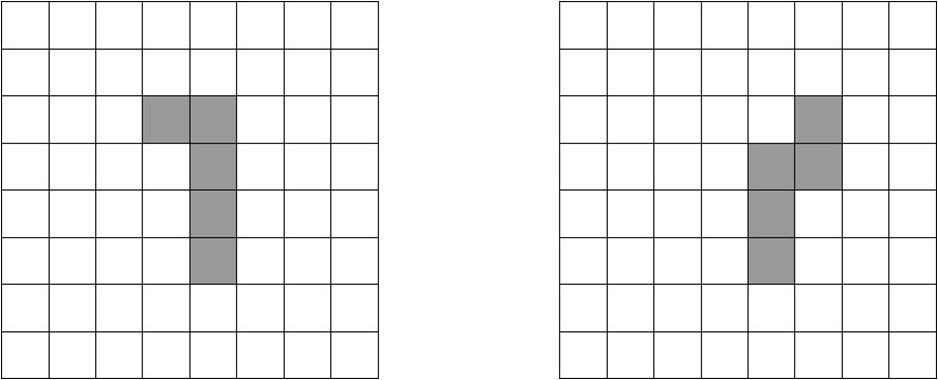
In the modification of the rules that I suggested, players must continue alternating selections after choosing their first piece. Notwithstanding that play has not yet commenced, it would seem that the first player can always select an appropriate piece to counter the second player’s selection, provided the first player knows by memory or can compute a winning continuation.
It is also interesting that, in Orman’s proof, “winning” means truly winning (at the game level, i.e. by placing an extra piece, since if the second player cannot place a piece, then the first player will have placed one additional piece).
The applicability of Orman’s proof is based on the availability of a winning first move for more than one choice of first piece selected, followed by forced best continuations. If the proof applies to the modified rules that I proposed, as I believe it does, then in a set or match consisting of either two or four games in which the players alternate placing first, the outcome would be a theoretical tie.
On the other hand, humans are not computers and I do not think that human players would be able to calculate a forced win from the first move in Pentominoes, for every possible counterplay. However, knowledge of the proof’s strategy might be helpful, and knowledge of the theoretical outcome might constitute a psychological advantage.
The Delphi implementation of Pentominoes and Hexominoes for Windows may be downloaded from here. By default, the game starts up in the Pentominoes mode (order 5 game). The icons on the three buttons at the center bottom of the form are supposed to suggest the numbers 4 - 5 - 6.

Clicking one of these buttons starts a new game of the selected order. There is no piece selection phase in the computer game. Instead, pieces are distributed randomly. If the player does not like the pieces that were dealt, it is easy to start another game, with a fresh distribution of pieces.
Either player can go first. To make the computer play first, click the Pass button. When you click a piece to be placed on the board, the program will display the symmetries of that piece immediately below the board on the form. For example -
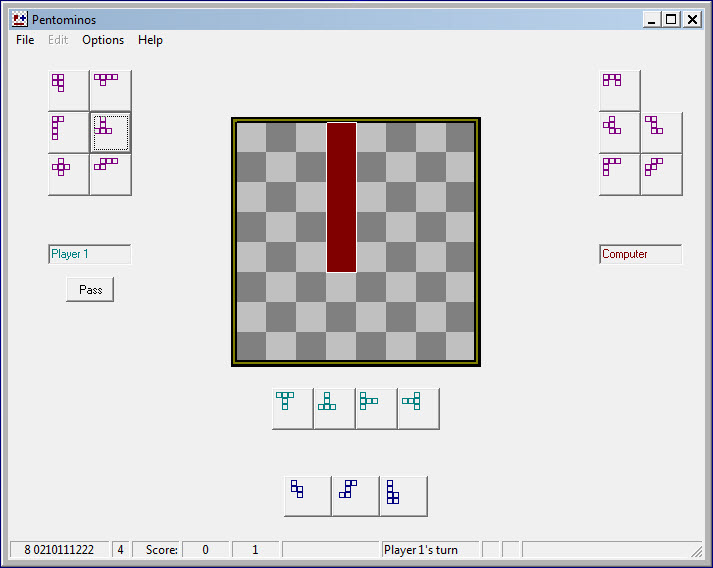

 In the illustration above, the human player first clicked Pass.
The program then placed the I-pentomino in the location
shown.
Next the human player selected the T-pentomino, with a view
to
creating a sanctuary for the P-pentomino. At the point of the
illustration the program has displayed the four symmetries of the
T-pentomino below the board. Next, the human player will
click
the rightmost symmetry. This causes the program to paint a
yellow
marker for the chosen symmetry as close to the top left corner of the
board as is possible (illustration at left). The play is not
yet
complete. Next the human player clicks on the yellow marker
(a
moving hand icon will appear) and drags it to the desired location on
the board. When finished with placement, the player clicks
the
piece once more to indicate that the move is complete. The
program will immediately reply with its next move (illustration at
right). Perhaps this example would have been clearer had the program
moved somewhere else, away from the corner. Nevertheless, the
example shows that the human player has successfully created a
sanctuary for one of his unplayed pieces. Sometimes when the
board is full of pieces more than one click-and-drag try may be needed
to move a piece to its final placement. The player's turn
does
not end until the piece has been clicked in place.
The rest is easy.
In the illustration above, the human player first clicked Pass.
The program then placed the I-pentomino in the location
shown.
Next the human player selected the T-pentomino, with a view
to
creating a sanctuary for the P-pentomino. At the point of the
illustration the program has displayed the four symmetries of the
T-pentomino below the board. Next, the human player will
click
the rightmost symmetry. This causes the program to paint a
yellow
marker for the chosen symmetry as close to the top left corner of the
board as is possible (illustration at left). The play is not
yet
complete. Next the human player clicks on the yellow marker
(a
moving hand icon will appear) and drags it to the desired location on
the board. When finished with placement, the player clicks
the
piece once more to indicate that the move is complete. The
program will immediately reply with its next move (illustration at
right). Perhaps this example would have been clearer had the program
moved somewhere else, away from the corner. Nevertheless, the
example shows that the human player has successfully created a
sanctuary for one of his unplayed pieces. Sometimes when the
board is full of pieces more than one click-and-drag try may be needed
to move a piece to its final placement. The player's turn
does
not end until the piece has been clicked in place.
The rest is easy.
Addendum: The photo shows a set of 3D-printed Pentominoes that fit a 12 inch chessboard (1.5 inch squares). Pieces are 3.2 mm thick. The chessboard pictured is a vinyl rollup type, this one. However, any 12-inch board will do. This zip archive contains six 3D printer .stl files, each specifying two pieces. Pieces may be separated in the slicer and printed individually. That is what I did, as our printer has a sweet spot where objects print more evenly and stick better to the bed. The pieces were designed in FreeCAD, where the unit square dimension and thickness were parameterized as spreadsheet cell values. It is recommended to avoid black and white or whatever are the colors of the board that will be used, in order that unoccupied squares are more easily seen. In the photo, square c5 is not occupied. If there were no gap at its bottom border this square might appear to be part of the ‘N’ pentomino.
The author makes no claim as to the accuracy or completeness of information presented on this page. In no event will the author be liable for any damages, lost effort, inability to reproduce a claimed result, or anything else relating to a decision to use the calculators or supplemental information on this page.
[0] A Java implementation of the VistA RPCB (called VistAlink) was released later.
[1] This project ultimately failed for a non-software reason. I attempted to fabricate a TTL to RS-232 hardware adapter. However, this effort was frustrating because the Yaesu FRG-100 uese a CAT connector (6-pin DIN socket) for its TTL-level data and I could not find a matching plug in Radio Shack. Therefore, I made one using a wooden dowel drilled with small holes for stiff wires to serve as pins. I got something wrong in the level conversion part—or possibly connected the pins incorrectly—and a diode blew on the first hookup. Luckily, the rest of the receiver was unharmed, except that the interface no longer worked. The computer's serial adapter was also unharmed—RS-232 interfaces were robust.
[2] May 1957 and October 1965. Also, The Scientific American Book of Mathematical Puzzles and Diversions, Fireside Books, New York, 1959.
[3] http://en.wikipedia.org/wiki/Pentomino.
[4] http://en.wikipedia.org/wiki/Tetris
[5] http://en.wikipedia.org/wiki/Solomon_W._Golomb
[6] Golomb, Solomon W., Polyominoes, Princeton University Press, 1994. ISBN: 0-691-08573-0
[7] Watkins, John J., Across the Board: The Mathematics of Chessboard Problems, Princeton University Press, 2004. (http://books.google.com/books/about/Across_the_Board.html?id=TtkLIE47DCkC)
[8] Watkins, John J. Ibid
[9] http://library.msri.org/books/Book29/files/orman.pdf
[10] This summary is considerably simplified. A sanctuary would only be counted if it did not duplicate a previously indexed sanctuary. The term sanctuary was originally suggested by Golomb.
.