Equinox Noon Sun


Chris shoots sun    Yesterday was the Spring Equinox (2014).  My friend and I brought the sextant to a nearby beach to shoot the noon sun.[1]  A passing beach-walker called out to us saying, “That looks like hard work—GPS would be easier.” In an age when our cell phones know which end of the park bench we are sitting on, why bother to shoot the sun? That is perhaps difficult to explain.

    There is just something appealing about deducing one’s latitude simply and directly, merely by observing the height of the sun at or near the time it crosses the celestial equator.  No complicated math is needed—no calculators or tables.  The calculation is as simple as subtracting the sun’s observed height from 90°.

    In centuries past mariners depended upon the noon sun for latitude.  An accurate timepiece was not needed because only the sun’s height matters for the noon latitude, not the time at which it reaches maximum height. It is necessary, however, to correct for the sun’s declination (angular distance north or south of the celestial equator).  

    The March 20, 2014 equinox occurred at 4:57 PM universal time (AKA Greenwich mean time), which corresponds to a few minutes before 1:00 PM EDT, where I live in Charleston, South Carolina. At the time of the equinox the sun’s declination is zero (by definition).  Charleston lies about 5° west of the 75° meridian.  Solar noon yesterday, the time that the sun reached its maximum height, was about a half hour after the equinox.  By then the sun was less than a minute north of the equator.  The exact time of solar noon for any location, as well as other interesting times, may be calculated at this NOAA page, from which the following table is reproduced.
Time of solar noon on the 2014 Spring Equinox

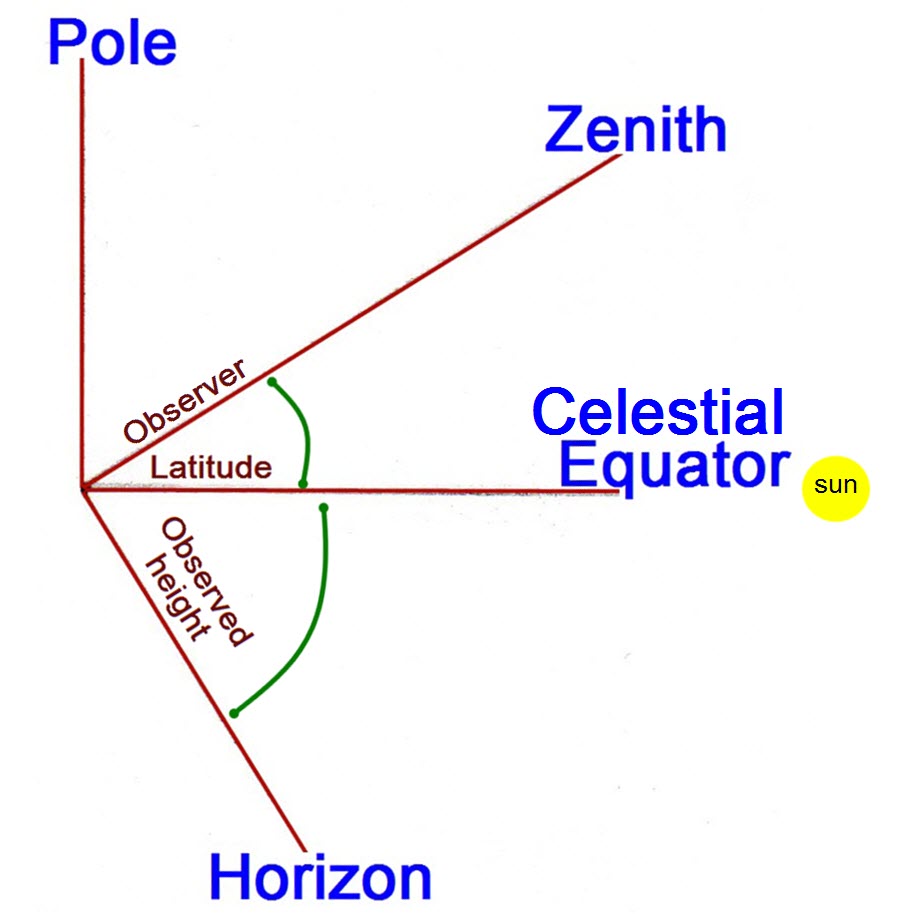
    Because solar noon occurred at nearly the same time as the equinox, declination can be ignored when computing latitude from yesterday’s noon sun. The simplicity of this situation is summarized in the sketch below.
Equinox sun

    The above diagram should be self-explanatory.  As we learned in school, earth’s equator is 90° from the pole—the same holds for the celestial poles and equator.  Similarly the horizon is 90° from the observer’s zenith, an imaginary point directly overhead in the sky.

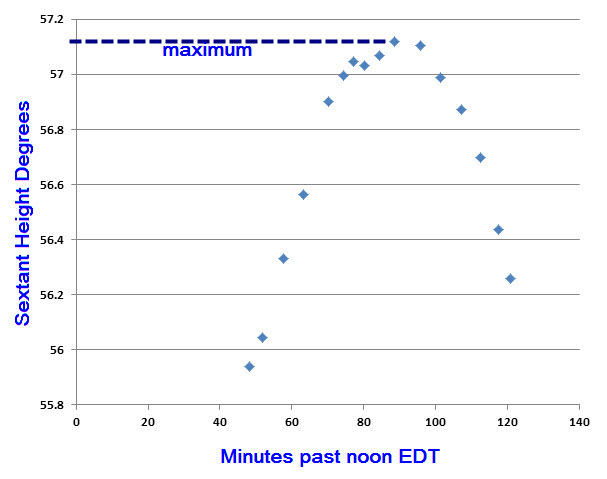
    When shooting sights yesterday, we did not know (or pretended not to know) exactly when the sun would reach its maximum height. We began taking sights at about ten minutes before 1 PM EDT and shot the last sight at about five past two.  This allowed us to plot a curve as the sun rose to its maximum height and then began to descend.  In the following graph, the horizontal axis is time in minutes past noon EDT and the vertical axis is sextant height (Hs) in degrees.  (Sextant height is uncorrected.)
Sextant Height Observations

Corrections for observed height    To compute observed height Ho from sextant height Hs, it is necessary to enter a few corrections. The largest correction is half the diameter of the sun.  The reason it is necessary to make this particular correction is that we measure the height of the sun’s lower limb (i.e., the point at which the lower limb appears to touch the horizon in the sextant view), while astronomical data, such as the time of the equinox, refer to the center of the sun. Rather than correct each individual observation, we corrected only the maximum sextant height, since that was the only point required for computing latitude.

    The DIP correction refers to the height of the observer’s eye.  The formula is 1.76 multiplied by the squareroot of height in meters. Lastly, the sextant zero point (where the reflected horizon makes a continuous line with the actual horizon) is a fraction of a minute below the zero mark on the scale.

    This brings us to the moment of truth, so-to-speak.  Subtracting 57° 22’ from 90° gives a latitude of 32° 38’. Our actual latitude by the park bench method[2] was 32° 35.5’.  Therefore we missed our latitude by 2.5’ (two and a half nautical miles). This degree of accuracy might be acceptable at sea, but seems rather unsatisfactory for observations from the beach, which is a perfectly stable platform.  We did not enter all corrections, however, I think the most likely explanation for the discrepancy is inaccuracy of the observations themselves.  The horizon was hazy and the sun partly obscured by sporadic wispy clouds.  Most of all, the navigator was inexperienced in the art of swinging the sextant—a skill that may be likened to bowing the violin.



[1] In the photo my friend Chris is taking a practice sight at Kiawah Island beach.
[2] GPS, of course.